|
Магнитное поле катушки с током возникает в кольцевой катушке (рис. 1) с W витками, равномерно распределенными вдоль немагнитного сердечника при подключении ее к источнику тока. Увеличение магнитной индукции поля достигается увеличением числа витков катушки и размещением ее на стальном сердечнике, магнитные токи которого, создавая свое поле, увеличивают результирующее поле катушки. Поверхность, ограниченная окружностью радиуса R, совпадающей со средней магнитной линией, пронизывается полным током ΣI = IW. Вследствие симметрии напряженность поля Н во всех точках, лежащих на средней магнитной линии, одинакова, поэтому мдс Fм = Hl = IW = H2πR. По закону полного тока Hl = IW, откуда напряженность магнитного поля на средней магнитной линии, совпадающей с осевой линией кольцевой катушки, H = IW / l , а магнитная индукция B = μaH = μaIW / l = 125μIW / l * 10-8.
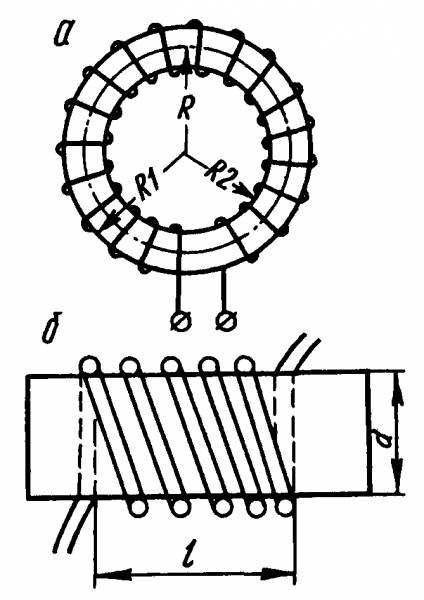
Рис. 1. Катушки индуктивности:
а - кольцевая; б - цилиндрическая
При R1 - R2 << Rl магнитную индукцию на осевой линии с достаточной точностью можно считать равной среднему значению ее, и, следовательно, магнитный поток сквозь поперечное сечение катушки Φ = BS = μaIWS / l . Переписав это уравнение в виде Φ = IW / (μaSl) = Fм / Rм , получим выражение, аналогичное уравнению закона Ома для электрической цепи, т.е. полный магнитный поток равен отношению мдс к магнитному сопротивлению цепи. Цилиндрическую катушку (рис. 1, б) можно рассматривать как часть кольцевой катушки с большим радиусом и с обмоткой, расположенной только на части сердечника, длина которой равна длине катушки. Напряженность поля и магнитной индукции на осевой линии в центре цилиндрической катушки определяется по формулам, которые в этом случае являются приближенными и применимы для катушек.
| 